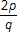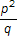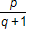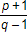Study Guide
Field 212: Multi-Subject: Teachers of Early Childhood
(Birth–Grade 2)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Selected-Response Questions
The following reference material will be available to you during the test:
Competency 0001
Number and Operations
1. Given that p and q are distinct prime numbers greater than 2, which could be a whole number?
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to apply number theory concepts. Prime numbers are numbers whose only factors are the number 1 and the number itself. Choose prime numbers and test them in each of the expressions. For example, if p equals 7 and q equals 7 then the only expression that represents a whole number is choice D: seven plus one over five minus one equals 2.
Competency 0001
Number and Operations
2. Which number represents the greatest quantity?
- the cube root of 0.216
- the non-terminating decimal 0.58, where the digit 8 repeats
- the square root of 0.24
- the fraction 1 over 30
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. This question requires the examinee to analyze and compare decimals and fractions. Determining the greatest quantity is aided by having the responses in decimal form. The cube root of 0.216 is a number that multiplied by itself 3 times equals 0.216, so the cube root of 0.216 is equivalent to 0.6. the square root of 0.24 can be estimated to be less than 0.5, since 0.24 is less than 0.25, and the fraction 1 over 30 is equivalent to 0.03. The greatest quantity out of all the responses is the cube root of 0.216.
Competency 0002
Operations and Algebraic Thinking
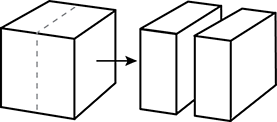
3. Use the diagram below to answer the question that follows.
An artist creates a cube using a piece of clay. The artist then cuts the cube in half to make two congruent rectangular solids, as shown in the diagram. Which is the ratio of the surface area of the original cube to the total surface area of the resulting rectangular solids?
- 1 to 2
- 2 to 3
- 3 to 4
- 5 to 6
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to solve unit-rate problems including those involving ratios of areas. Since the original solid is a cube, its surface area is 6 times the area of one face. Suppose the area of one face is 1 square unit, then the original surface area is 6 square units. By cutting the cube in half, the artist has created two new surfaces, each with area 1 square unit, and kept the other surfaces the same. Thus the total area of the two solids is 8 square units. The ratio of the original surface area to the new total surface area is 6 to 8 or 3 to 4.
Competency 0002
Operations and Algebraic Thinking
4. The expression 16 minus 4 divided by 1 fourth plus 1 simplifies to which integer?
- 49
- 16
- 4
- 1
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to apply operations and relationships between operations. According to the order of operations, division should occur first when simplifying this expression. Dividing 4 by 1 fourth is 16. The equation then becomes 16 minus 16 plus 1 = 1.
Competency 0003
Measurement, Geometry, and Data
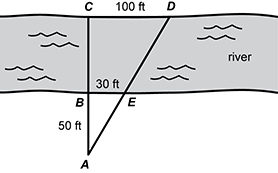
5. Use the diagram below to answer the question that follows.
river with several points labeled. point a is on the bank point b is on the bank of the river on the southern side the distance between a and b is fifty feet c is directly across the river on the northern bank there are line segments connecting a b and c. point d is on the bank to the right one hundred feet of point c point e is thirty feet to the left of point b there are line segments drawn to connect d e and a. the line segments make triangle a c d with being a line segement through the triangle and side a d being the hypotenuse
The diagram represents a method for estimating B C, the width of a river. Given that A B equals 50 feet, C D equals 100 feet and B E equals 30 feet, which is the best estimate for B C ?
- 60 feet
- 80 feet
- 117 feet
- 167 feet
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to solve problems involving similarity. Triangle A B E is similar to Triangle A C D because their corresponding angles are congruent. Therefore the corresponding sides of the two triangles are proportional: fifty over a c equals thirty over one hundred, and 30 left paren A C right paren equals 5000. To the nearest foot, A C is 167, so B C is 167 minus 50 or 117 feet.
Competency 0003
Measurement, Geometry, and Data
6. Use the diagram below to answer the question that follows.
A rectangle is shown. Its perimeter is 85 feet and its width is 19 feet.
Given the dimensions shown in the diagram, what is the area of the rectangle?
- 446.5 F T squared
- 893 F T squared
- 1,706 F T squared
- 1,997.5 F T squared
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. This question requires the examinee to solve a mathematical problem involving perimeter and area. The area of a rectangle is determined by multiplying its length by its width. In this problem, the width of the rectangle is given (19 ft.), but the length of the rectangle must be calculated. Since the perimeter of a rectangle is the sum of all four sides, and the two shorter sides equal a combined 38 ft., the length of the rectangle must be 85 ft. (the stated perimeter) minus 38 ft. (the sum of the two shorter sides), which equals 47 ft. Dividing the length of the two longer sides by 2 equals 23.5 ft. Now the area can be determined by multiplying 23.5 ft. (the length) times 19 ft. (the width), which yields 446.5 F T squared.
Competency 0004
Instruction in Mathematics
7. Use the diagram below to answer the question that follows.
A teacher places a set of blocks on a table and asks a child how many blocks there are. The child points to each block while saying the numbers in the proper sequence from one through five. When asked again how many blocks there are, the child responds by counting the number of blocks again. Given this evidence, which question could the teacher ask to help the child connect counting to cardinality?
- How many cones, boxes, and balls are there?
- How is the last number name you said related to the number of blocks?
- How many different types of shapes are there?
- How is the first block counted similar to the last block counted?
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to apply strategies for teaching counting and cardinality. The number of objects in a group is the cardinal number, or cardinality, of the group. When counting the objects in a group, the last number named is the number of objects in the group.
Competency 0004
Instruction in Mathematics
8. Use the excerpt below from an exit ticket to answer the question that follows.
Compare the numbers in each row using less than, =, greater than.
Sample 567 is less than 576 1. 489 blank 490 2. 112 blank 102 3. 320 blank 302 4. 864 blank 846 5. 975 blank 798
The excerpt shows the first 5 problems from a series of 20 similar problems on an exit ticket for second-grade students. Previously, the class spent time discussing the meanings of the inequality symbols greater than and less than. The students will complete the exit ticket independently and then swap their papers with a classmate to check each other's work. The purpose of this activity is to build students' understanding of:
- number operations.
- place-value concepts.
- the use of the equal sign.
- the meaning of equations.
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to demonstrate knowledge of strategies for teaching place value concepts. The numbers of each pair contain two or three shared digits that are not necessarily in the same place value position. This requires the student to look closely at the place value of the numbers and go beyond the hundreds place to the tens and ones places to determine which quantity in each pair of numbers is greater than, less than, or equal to its counterpart.