Study Guide
Field 212: Multi-Subject: Teachers of Early Childhood
(Birth–Grade 2)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Constructed-Response Item 1
Competency 0005
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the assignment that follows.end bold
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Background Information
First-grade students have been developing an understanding of adding two single-digit numbers and representing the process as an equation. The students have been adding and subtracting within 20 using strategies such as counting on, making ten, and decomposing a number leading to a ten. The class is currently working on the following standard from the New York State P through 12 Learning Standards for Mathematics.1
start bold Operations & Algebraic Thinking (UCARTAP NY-1.OA) end bold
start bold Work with addition and subtraction equations. end bold
7. Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false.
The teacher has planned a lesson experience in which students will use number cards and recording sheets. The teacher has the students work in groups of two.
Description of Class Activity
In the teacher's lesson experience, pairs of students practice combining two numbers while playing a game called "Capture 4." The teacher gives each pair of students a deck of illustrated number cards and recording sheets for writing equations involving addition. The cards are numbered from 0 to 9. To play the game, each student turns over two number cards, finds the sum of the two numbers on the cards, and then writes an equation for the addition problem on the recording sheet. The player with the largest sum "captures" all four cards. Two cards and a completed recording sheet are shown in the example below.
Capture 4 Recording Sheet
Name: StudentWrite your equation below. 8 plus 6 equals 14
Excerpt of Group Discussion
As students work, the teacher moves among them to observe their activity and ask questions. The teacher notices that students use a variety of adding strategies. For example, some students count using the dots on both cards, and others start with the total on one card and then count up using the dots on the other card. The teacher stops to observe one group's work in progress and asks the students to explain their strategies for computation. The group's work is shown below, accompanied by an excerpt of a discussion between the two partners and the teacher.
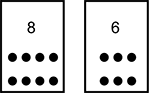
Kaleme and Isabella have turned over the following cards.
Kaleme has two cards, one with seven dots and one with eight. Isabella also has two cards, one with six dots and one with five.
Kaleme: I won! Isabella: Wait, that's too fast. How did you add them up so fast? Kaleme: I didn't have to add. My cards have more dots than yours, so I must have more. Isabella: That's not fair. You still have to add them up and write the equations down. Then it's my turn, and then we decide who won. The teacher observes as Kaleme covers two of the dots on the 7 card with his finger and counts the remaining dots.
Kaleme: (counts out loud) 1, 2, 3, 4, 5. I have 15. The teacher decides to intervene and ask Kaleme some questions.
Teacher: Can you explain how you got your total, Kaleme? Kaleme: I knew that I needed 2 more to make 10 on the 8 card. So, I took 2 off of the 7 card (illustrates this by covering two of the dots again). Then I just counted what's left on the 7 card: 1, 2, 3, 4, 5. So, 10 with 5 more is 15. So, now I can record it. Kaleme fills out his recording sheet as shown below.
Capture 4 Recording Sheet
Name: KalemeWrite your equation below. 8 plus 2 equals 10 plus 5 equals 15
Teacher: I agree with the sum that you found but let's look closer at the equation. Kaleme: I think the equation is right because it is true that 8 plus 2 equals 10 and 10 plus 5 equals 15 . Those are easy sums to figure out.
Sample Strong Response to Constructed-Response Item 1
Kaleme demonstrates a significant mathematical strength in his ability to decompose
a number leading to a ten. With this knowledge he appears to be able to apply the
associative property to draw his conclusion that his two cards have more dots than
his partner's. Knowing 2 more than 8 was needed to make 10, Kaleme decomposed 7 to
Kaleme demonstrated a significant area of need in his misuse of the equality symbol, using " the equal sign " as an arrow leading to an answer to a computation, rather than as a symbol meaning that the expressions on either side of it must have the same value. After writing " 8 plus 2 equals 10 plus 5 equals 15 " Kaleme says it is true because " 8 plus 2 equals 10 and 10 plus 5 equals 15.
Instructional intervention should build on Kaleme's understanding of the associative
property and help clarify the meaning of the equality symbol. Asking "What does
= mean?" would be a first step toward assessing what the student is thinking. The
teacher would then work with Kaleme on his erroneous equation and discuss what is
right with it. Kaleme sees that
8 plus 2 equals 10
10 plus 5 equals 15
Following the logical progression of his own statements and then analyzing the flawed logic resulting from the misused equality sign when it is pointed out to him will help Kaleme build a viable argument.
Kaleme should practice this by playing a matching game that includes cards with
equations on them such as
4 plus 2,
and
3 plus 3,
etc., and cards with an equal sign. He would make equations, illustrating that what was
on one side of the equal sign was, in fact, equal to what was on the other side:
3 plus 3 equals 4 plus 2,
3 plus 7 equals 10
10 plus 6 equals 16
Throughout the activity, the teacher should continue to ask the student to explain the meaning of the equals symbol and describe what he is doing.
Sample Constructed-Response Item 2
Competency 0005
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the assignment that follows. end bold
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Background Information
Prekindergarten children have been developing an understanding of the different kinds of shapes with straight sides, including squares, rectangles, and triangles. The class is currently working on the following standard from the New York State Pthrough12 Learning Standards for Mathematics.2
start bold Geometry (NY-PK.G) end bold
start bold Identify and describe shapes (squares, circles, triangles, and rectangles). end bold
2. Name shapes regardless of size.
Description of Class Activity
The teacher has set up an interactive lesson experience during which children will use sticks and straws to create squares, triangles, and rectangles and name each shape. The children will work in groups of two. The teacher walks throughout the room to observe the way the children interact with one another and create models, gathering information to determine whether the class is ready to move to a new topic or identify any common misconceptions that need to be addressed.
Excerpt of Group Discussion
Teacher: Wow, you have been busy! Can you tell me what you've made? One of the students, Kinsey, points to her four shapes, which are shown below.
An image of four shapes arranged in a line is shown. The first two shapes are squares and the last two shapes are equilateral triangles. The left square is much larger than the other shapes. The left equilateral triangle has a vertex pointing up, the right equilateral triangle has a vertex pointing down.
Kinsey: I made four shapes. Teacher: Can you tell me what they are? Kinsey: This is a square (points to the small square). This is a rectangle (points to the big square). This is a triangle (points to the small triangle). This is a different triangle (points to the upside-down triangle). Teacher: (points to the first two shapes) How did you know to call these a square and a rectangle? Kinsey: Squares and rectangles have four sides. These shapes have four sides. And, they look like boxes. Rectangles are bigger than squares. The bigger one with four sides is a rectangle. The little one with four sides is a square. Teacher: How did you know to call the shapes "triangles"? Kinsey: Triangles only have three sides. These are different because one is pointing up, and one is upside down.
Sample Strong Response to Constructed-Response Item 2
The student shows a significant mathematical strength in that she can recognize the difference between a three-sided shape and a four-sided shape, identifying two squares as shapes with four sides and the two triangles as shapes with three sides. She notes that the shapes she identifies as square and rectangle each have four sides and look like boxes, relating their shape to something she is familiar with - a box. While she refers to one of the triangles as different because it is upside down, she still sees it as a triangle because it has three sides. The orientation of the triangle does not affect her understanding of them both as triangles. She also understands the names of the four different shapes she has made in relation to the shapes her class is learning about, and she is partially correct in her description of a rectangle.
Kinsey has a significant mathematical area of need when it comes to recognizing the difference between a square and a rectangle. While she understands that both shapes have four sides, she believes that the difference between a rectangle and a square is that a rectangle is bigger, and therefore calls the bigger square she has made a rectangle. This may be because she has been told that a rectangle has four sides, with two sides bigger than the other two sides, but it has caused a misunderstanding that a rectangle is simply bigger.
As an intervention, I would start by having Kinsey tell me again what the similarities are between the two square shapes she has made. She will repeat that they both have four sides, which she has already identified. I would then review with her that a rectangle has four sides, but that with a rectangle two sides are the same length as each other as are the other two sides, but that one set of sides is longer - or bigger - than the other set of sides. I would then make a rectangle, using other straws, to illustrate what this looks like, and I will have her note that there are two shorter sides and two longer - or as she has called them, bigger - sides. I will then point to different rectangles nearby - a piece of paper for example - and ask her what the shape is and have her explain how she can tell the shape is a rectangle (four sides, with two sides longer than the other two sides). From here, I will work with Kinsey and her partner to make several four-sided shapes having them identify whether the shape is a square or a rectangle. I will want her to be able to show me that the two sets of sides are different lengths in a rectangle, but they are all the same length in a square. As a follow-up activity, I will have Kinsey find objects in the room that are either rectangles or squares, and have her describe which shape is which, while explaining how she can tell the difference between the two.
Performance Characteristics for Constructed-Response Item
The following characteristics guide the scoring of the response to a constructed-response item.
| Completeness | The degree to which the response addresses all parts of the assignment |
|---|---|
| Accuracy | The degree to which the response demonstrates the relevant knowledge and skills accurately and effectively |
| Depth of Support | The degree to which the response provides appropriate examples and details that demonstrate sound reasoning |
Score Scale for Constructed-Response Item
A score will be assigned to the response to a constructed-response item according to the following score scale.
| Score Point | Score Point Description |
|---|---|
| 4 |
The "4" response reflects a thorough command of the relevant knowledge and skills:
|
| 3 |
The "3" response reflects a general command of the relevant knowledge and skills:
|
| 2 |
The "2" response reflects a partial command of the relevant knowledge and skills:
|
| 1 |
The "1" response reflects little or no command of the relevant knowledge and skills:
|
| U | The response is unscorable because it is unrelated to the assigned topic or off task, unreadable, written in a language other than English or contains an insufficient amount of original work to score. |
| B | No response. |
Acknowledgments
1From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Internet. Available from http://www.nysed.gov/curriculum-instruction/new-york-state-next-generation-mathematics-learning-standards; accessed 6/4/2020.
