Study Guide
Field 246: Multi-Subject: Teachers of Early Childhood
(Birth–Grade 2)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Selected-Response Questions
The following reference material will be available to you during the test:
Competency 0001
Number and Operations
1. Use the student work below to answer the question that follows.
Step 1: 4.8 times 0.5 =
Step 2: the quantity 4 plus 0.8 times 0.5 =
Step 3: 4 times 0.5 + 0.8 times 0.5 =
Step 4: 2 + 0.4 = 2.4
Step 3 of this work indicates an understanding of which concept?
- associative property
- commutative property
- distributive property
- multiplicative inverse property
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. Multiplying each addend separately and then adding the products to arrive at a final answer shows an understanding of the distributive property. Step 3 in the student work sample shows the distributive law in action when the addend of 4 is multiplied by 0.5 (4 times 0.5) separately from the addend 0.8 (0.8 times 0.5).
Competency 0001
Number and Operations
2. Which number represents the greatest quantity?
- the cube root of 0.216
- the non-terminating decimal 0.58, where the digit 8 repeats
- the square root of 0.24
- the fraction 1 over 30
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. This question requires the examinee to analyze and compare decimals and fractions. Determining the greatest quantity is aided by having the responses in decimal form. The cube root of 0.216 is a number that multiplied by itself 3 times equals 0.216, so the cube root of 0.216 is equivalent to 0.6. the square root of 0.24 can be estimated to be less than 0.5, since 0.24 is less than 0.25, and the fraction 1 over 30 is equivalent to 0.03. The greatest quantity out of all the responses is the cube root of 0.216.
Competency 0001
Number and Operations
3. Which expression is equivalent to 1 and three quarters times 3 and 5 sixths?
- open paren 1 times 3 close paren times open paren 3 quarters times 5 sixths close paren
- open paren 1 plus 3 close paren times open paren 3 quarters plus 5 sixths close paren
- 3 times open paren 1 plus 3 quarters close paren plus 1 times open paren 3 plus 5 sixths close paren
- 3 times open paren 1 plus 3 quarters close paren plus 5 sixths times open paren 1 plus 3 quarters close paren
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. An equivalent expression looks different from an initial expression but will produce the same answer. The initial expression 1 and three quarters times 3 and 5 sixths is equivalent to the expression 3 times open paren 1 plus 3 quarters close paren plus 5 sixths times open paren 1 plus 3 quarters close paren as the mixed numbers are shown as a sum of their digit and fraction components and then the distributive property is applied.
Competency 0002
Operations and Algebraic Thinking
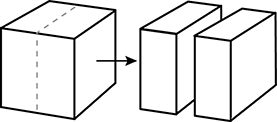
4. Use the diagram below to answer the question that follows.
An artist creates a cube using a piece of clay. The artist then cuts the cube in half to make two congruent rectangular solids, as shown in the diagram. Which is the ratio of the surface area of the original cube to the total surface area of the resulting rectangular solids?
- 1 to 2
- 2 to 3
- 3 to 4
- 5 to 6
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to solve unit-rate problems including those involving ratios of areas. Since the original solid is a cube, its surface area is 6 times the area of one face. Suppose the area of one face is 1 square unit, then the original surface area is 6 square units. By cutting the cube in half, the artist has created two new surfaces, each with area 1 square unit, and kept the other surfaces the same. Thus the total area of the two solids is 8 square units. The ratio of the original surface area to the new total surface area is 6 to 8 or 3 to 4.
Competency 0002
Operations and Algebraic Thinking
5. The expression 16 minus 4 divided by 1 fourth plus 1 simplifies to which integer?
- 49
- 16
- 4
- 1
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to apply operations and relationships between operations. According to the order of operations, division should occur first when simplifying this expression. Dividing 4 by 1 fourth is 16. The equation then becomes 16 minus 16 plus 1 = 1.
Competency 0002
Operations and Algebraic Thinking
6. Which word problem could be solved using the expression 14 times open paren 7 plus 6 close paren?
- A baker makes 7 cakes in the morning and 6 cakes in the afternoon, every day for 14 days. How many cakes are made in all?
- A carpenter builds 7 chairs and sells 6 every other day for 14 days. How many chairs are sold in all?
- In one day, a florist sells 7 floral arrangements. On the next, the florist sells 6. If arrangements continued to be sold following this pattern for 14 days, how many arrangements are sold in all?
- On one day, a barbershop has 14 regular customers. Advertising brings in 7 new customers, and 6 more come from recommendations. How many customers does the barbershop have in all that day?
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. The baker made 7 cakes in the morning and 6 cakes in the afternoon, or the quantity 7 plus 6. The baker repeated this process for 14 days. This is shown as 14 times open paren 7 plus 6 close paren.
Competency 0003
Measurement, Geometry, and Data
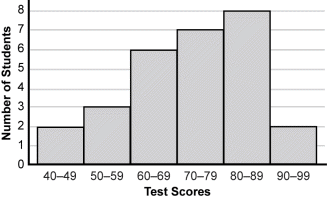
7. Use the histogram below to answer the question that follows.
A histogram is shown. The vertical axis is labeled Number of Students and the horizontal axis is labeled Test Scores. 2 students have scores in the range from 40 to 49, 3 from 50 to 59, 6 from 60 to 69, 7 from 70 to 79, 8 from 80 to 89, and 2 from 90 to 99.
Given the histogram showing the test scores students earned on a recent exam, which statement is a valid conclusion?
- No student earned a score of 40.
- The mean score is in the eighties .
- At least one student earned a score of 100.
- The median score is in the seventies .
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. The median is the middle value in a sorted numerical data set. There are a total of 2 + 3 + 6 + 7 + 8 + 2 = 28 values in the set. For this set, which has an even number of values, the median occurs at the average value of data points 14 and 15. Both of these values fall in the range between 70 and 79, so the median score is in the seventies .
Competency 0003
Measurement, Geometry, and Data
8. Use the diagram below to answer the question that follows.
A rectangle is shown. Its perimeter is 85 feet and its width is 19 feet.
Given the dimensions shown in the diagram, what is the area of the rectangle?
- 446.5 F T squared
- 893 F T squared
- 1,706 F T squared
- 1,997.5 F T squared
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. This question requires the examinee to solve a mathematical problem involving perimeter and area. The area of a rectangle is determined by multiplying its length by its width. In this problem, the width of the rectangle is given (19 ft.), but the length of the rectangle must be calculated. Since the perimeter of a rectangle is the sum of all four sides, and the two shorter sides equal a combined 38 ft., the length of the rectangle must be 85 ft. (the stated perimeter) minus 38 ft. (the sum of the two shorter sides), which equals 47 ft. Dividing the length of the two longer sides by 2 equals 23.5 ft. Now the area can be determined by multiplying 23.5 ft. (the length) times 19 ft. (the width), which yields 446.5 F T squared.
Competency 0003
Measurement, Geometry, and Data
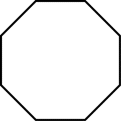
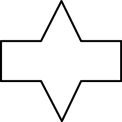
9. Which shape has exactly 4 lines of symmetry?
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. A line of symmetry is an invisible line that, when placed through the center of an object, will divide the object into equal identical halves or partitions. The shape in response C has four lines of symmetry that would divide the shape into four identical partitions. One line is horizontal, a second is vertical, a third is diagonal from the left, and a fourth is diagonal from the right.
Competency 0004
Instruction in Mathematics
10. Use the diagram below to answer the question that follows.
A teacher places a set of blocks on a table and asks a child how many blocks there are. The child points to each block while saying the numbers in the proper sequence from one through five. When asked again how many blocks there are, the child responds by counting the number of blocks again. Given this evidence, which question could the teacher ask to help the child connect counting to cardinality?
- How many cones, boxes, and balls are there?
- How is the last number name you said related to the number of blocks?
- How many different types of shapes are there?
- How is the first block counted similar to the last block counted?
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to apply strategies for teaching counting and cardinality. The number of objects in a group is the cardinal number, or cardinality, of the group. When counting the objects in a group, the last number named is the number of objects in the group.
Competency 0004
Instruction in Mathematics
11. Use the excerpt below from an exit ticket to answer the question that follows.
Compare the numbers in each row using less than, =, greater than.
Sample 567 is less than 576 1. 489 blank 490 2. 112 blank 102 3. 320 blank 302 4. 864 blank 846 5. 975 blank 798
The excerpt shows the first 5 problems from a series of 20 similar problems on an exit ticket for second-grade students. Previously, the class spent time discussing the meanings of the inequality symbols greater than and less than. The students will complete the exit ticket independently and then swap their papers with a classmate to check each other's work. The purpose of this activity is to build students' understanding of:
- number operations.
- place-value concepts.
- the use of the equal sign.
- the meaning of equations.
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to demonstrate knowledge of strategies for teaching place value concepts. The numbers of each pair contain two or three shared digits that are not necessarily in the same place value position. This requires the student to look closely at the place value of the numbers and go beyond the hundreds place to the tens and ones places to determine which quantity in each pair of numbers is greater than, less than, or equal to its counterpart.
Competency 0004
Instruction in Mathematics
12. Use the problem below to answer the question that follows.
A student had 17 marbles, but then lost some of them. Now the student has 5 marbles. How many marbles did the student lose?
Students in a first-grade class independently solve the word problem. The teacher notices some students record 22 marbles as the answer. Which strategy would best help the teacher address these students' misunderstanding?
- having students use tally marks to count on from the smaller number
- suggesting that students rewrite the problem by stacking the numbers vertically
- drawing to model similar problems for the class using a part-part-whole model
- explicitly instructing students to subtract the smaller number from the larger number
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. Subtraction and addition are often taught as part-part-whole problems because students work with two different quantities (parts) to find their sum (whole). Presenting addition and subtraction using the part-part-whole model provides students with a visual representation for the processes of putting together or taking away. Pairing the part-part-whole model for this word problem with drawn models will engage the students in grade-level-appropriate practices that support their subtraction and addition skills.