Study Guide
Field 004: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Selected-Response Questions
The following reference material will be available to you during the test:
Competency 0001
Number and Quantity
1. Use the information below to answer the question that follows.
Two matrices, A and B Matrix A start three by three matrix first row first column A subscript eleven second column A subscript twelve third column A subscript thirteen second row first column A subscript twenty one second column A subscript twenty two third column A subscript twenty three third row first column A subscript thirty one second column A subscript thirty two third column A subscript thirty three end matrix Matrix B start three by three matrix first row first column A subscript eleven second column A subscript twelve third column A subscript thirteen row two first column A subscript thirty one second column A subscript thirty two third column A subscript thirty three third row first column A subscript twenty one second column A subscript twenty two third column A subscript twenty three end matrix.
Matrix B is composed of the elements from matrix A, as shown above. Which statement describes the relationship between the determinants of the two matrices?
- determinant of matrix B equals determinant of matrix A
- determinant of matrix B equals negative determinant of matrix A
- Determinant of matrix B equals one over determinant of matrix A
- Determinant of matrix B equals negative one over determinant of matrix A
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to demonstrate understanding of the properties of matrices. Rows 2 and 3 of matrix A have been interchanged to form matrix B. A theorem from linear algebra states: "If matrix B results from interchanging two rows or two columns of matrix A, then determinant of matrix B equals negative determinate of matrix A." Alternatively, calculate each determinant. Determinant of matrix A equals, A subscript 11, A subscript 22, A subscript 33, plus A subscript 12, A subscript 23, A subscript 31, plus A subscript 13, A subscript 21, A subscript 32, minus A subscript 11, A subscript 23, A subscript 32, minus A subscript 12, A subscript 21, A subscript 33, minus A subscript 13, A subscript 22, A subscript 31. determinant of matrix B has the same six products as determinant of matrix A , but with opposite signs, so determinate of matrix B equals negative determinant of matrix A .
Competency 0001
Number and Quantity
2. Which property justifies the process of simplifying a fraction to an equivalent fraction in lowest terms?
- the multiplication property of equality
- the symmetric property of equality
- the multiplicative identity property of real numbers
- the closure property of multiplication of real numbers
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. The question requires the examinee to apply understanding of arithmetic to the rational numbers. Fractions are real numbers, and all real numbers possess the multiplicative identity property: a number and its product with 1 are identical. For this property do more than restate the original number, such as with , Six-eighths times 1 is six-eighths substitute 1 with an equivalent fraction that simplifies the original numerator and denominator. In this case, replace 1 with 1 half divided by 1 half and then multiply: 6 eighths times 1 half divided by 1 half = 6 halves divided by 8 halves, which is 3 fourths .
Competency 0001
Number and Quantity
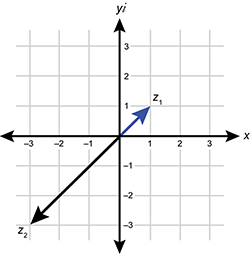
3. Use the graph below to answer the question that follows.
A complex plane with two arrows, one labeled z sub 1, and the other labeled z sub 2. The arrow labeled z sub 1 begins at the original and ends one unit to the right and one unit up. The arrow labeled z sub 2 also begins at the origin and terminates three units left and three units down.
The graph shows the complex plane and two numbers, z sub 1 and z sub 2 . What is the polar form of the product z sub 1 z sub 2 ?
- 6 times the quantity of open paren the cosine of one half pi plus i times the sine of one half pi close paren;
- 6 times the quantity of open paren the cosine of three-halves pi plus i times the sine of three-halves pi. close paren;
- 6 times the square root of 2 times quantity of open paren the cosine of five-fourths pi plus i times the sine of five-fourths pi close paren;
- 6 times the square root 2 times quantity of open paren the cosine of seven-fourths pi plus i times the sine of seven-fourths pi close paren;
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to perform operations with complex numbers and represent these numbers in the complex plane. The graph shows that z sub 1 is one plus I and z sub 2 is negative three minus three I The product z sub 1 z sub 2 is the quantity one plus I times the quantity negative 3 minus 3i equals zero minus 6i is represented by a vector of length 6 on the negative imaginary axis or the point zero comma negative 6 The polar angle is 270 degrees counter clockwise from the positive real axis, or three-halves pi in radians. The polar form can be expressed as r times the quantity cosine theta plus I sine theta so z sub 1 times z sub 2 is 6 times the quantity of open paren the cosine of three-halves pi plus i times the sine of three-halves pi close paren
Competency 0002
Algebra
4. Which equation could be a step in finding the points of intersection of the graphs of the curves given by y equals 2 x squared minus 2 x plus 8 and y equals 4 x squared minus 6 x plus 3 when using the method of completing the square?
- left paren x minus 2 right paren squared equals 5 over 2
- left paren x minus 1 right paren squared equals 6 over 2
- left paren x minus 1 right paren squared equals 7 over 2
- left paren x minus 2 squared equals 9 over 2
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to rewrite expressions in equivalent forms. To find the points of intersection, write 2 x squared minus 2 x plus 8 equals 4 x squared minus 6 x plus 3 and use the properties of equality to rewrite this equation as 2 x squared minus 4 x minus 5 equals 0. Then complete the square so that left paren x squared minus 2 x plus 1 right paren minus 2 minus 7 equals 0 and 2 left paren x minus 1 right paren squared minus 7 equals 0. Finally, write left paren x minus 1 right paren squared equals 7 over 2
Competency 0002
Algebra
5. A horizontal beam supported on both ends can safely carry a uniformly distributed load whose weight varies jointly as the width of the beam and the square of its height, and inversely as the distance between supports. A beam 6 inches wide and 6 inches high with supports 12 feet apart can safely carry a load of 1800 pounds. If a beam of the same material is 6 inches wide but only 4 inches high, what distance between supports is needed to safely carry the 1800-pound load?
- 4.5 feet
- 5.3 feet
- 6.0 feet
- 8.0 feet
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to demonstrate knowledge of proportional relationships to solve real-world problems. Let width = w, height = h, distance between supports = d, and load = L. The relationship among the variables is L = , k times w times h squared divided by d where k is the constant of proportionality. Substituting values, 1800 = , k times 6 times 6 squared divided by 12 and solving for k yields k = 100. Substituting new values, 1800 = , 100 times 6 times 4 squared divided by d and solving for d yields d is approximately 5.3 feet.
Competency 0002
Algebra
6. Use the table below to answer the question that follows.
x open paren negative infinity , negative 2 close paren negative 2 open paren negative 2, 1 close paren 1 open paren 1, 5 close paren 5 open paren 5, 9 close paren 9 open paren 9, infinity close paren f of x negative 0 positive 0 positive 0 negative 0 negative
The table describes the y-values for various x-values of a polynomial f of x. The degree of f of x is:
- at most 4.
- exactly 4.
- exactly 6.
- at least 6.
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to demonstrate understanding of the relationship between zeros and factors of polynomials. The table shows four x-intercepts, so the linear factors of f of x are open paren x plus 2 close paren to the p power times open paren x minus 1 close paren to the q power time open paren x minus 5 close paren to the r power times open paren x minus 9 close paren to the t power . There may be quadratic factors that are irreducible over the real numbers and thus do not correspond to zeros of the polynomial. Since the y-values change sign on opposite sides of x is negative 2 , the factor (x + 2) must have odd multiplicity. Thus, p is an odd number greater than or equal to 1. The same is true of the factor x minus 5 , so r is odd and greater than or equal to 1. The factors x minus 1 and x minus 9 must have even multiplicity since the y-values have the same sign on opposite sides of x = 1 and x = 9. Thus, q is even and greater than or equal to 2, and t is even and greater than or equal to 2. Even without quadratic factors, the sum of the given exponents is greater than or equal to 6, so the degree of f of x is at least 6.
Competency 0003
Functions
7. Use the diagram below to answer the question that follows.
Wind turbine with three blades. Each blade is 12 meters long. Point P is located at the tip of a blade that is horizontal to the ground and is sixteen meters up from the ground.
The diagram above shows a wind turbine on a vertical shaft. The height of the shaft is 16 meters The length of a wind turbine blade is 12 meters Point P is located at the tip of one of the wind turbine blades. The wind turbine rotates in the counterclockwise direction at a constant rate of 1 revolution per second. At t equals 0, point P is located at a height of 16 meters above ground. Which function models the height of point P above ground as a function of t?
- f of t equals 12 cosine (2 pi t)
- f of t equals 16 cosine (pi t)
- f of t equals 12 sine (2 pi t) plus 16
- f of t equals 16 sine (pi t) plus 4
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to model periodic phenomena with trigonometric functions. The height can be modeled by either a sine wave or a cosine wave. Since the length of the blade is 12 meters, point P will rise to left paren 16 plus 12 right paren meters and fall to left paren 16 minus 12 right paren meters Thus, the amplitude, A, of the wave is 12 and the axis of the wave on a t-y coordinate plane is y equals 16. The period is 1 second and, using period equals 2 pi over B, B equals 2 pi, which is the coefficient of t in a sine wave or cosine function. At t equals 0, point P on the blade is at the height of the axis of the wave, so the sine function is the better choice. Using the general form of a sine wave, f of t equals A sine left paren B t right paren plus k and f of t equals 12 sine left paren 2 pi t right paren plus 16.
Competency 0003
Functions
8. What is the solution to the equation one minus the secant of x equals the tangent of x for all real values of x?
- x is the product of pi and n, where n is an integer
- x is the product of 2 and pi and n, where n is an integer
- x is the sum of one-half pi and pi times n, where n is an integer
- x is the sum of one-half pi and the product of 2 pi and n where n is an integer
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to apply trigonometric identities and to solve trigonometric equations. The identity one plus the square of the tangent of x is the square of the secant of x is a clue, which leads one to square both sides of the given equation. open paren 1 minus secant of x close paren quantity square is the square of the tangent of x, which becomes 1 minus 2 times the secant of x plus the square of the secant of x is the square of the tangent of x, which becomes 1 minus 2 times the secant of x plus 1 plus the square of the tangent of x, equals the square of the tangent of x . Simplifying and factoring yields two times the quantity open paren 1 minus the secant of x close paren is zero . Then the secant of x is 1 , which also means that the cosine of x is 1 and x = 0 radians. Since the period of the cosine function is 2 times pi, x is 0 plus 2 times pi times n for integer values of n.
Competency 0003
Functions
9. A bacterial population starts at 5000. After 30 minutes, there are 8000 bacteria. If the function y equals C e to the power of k times t represents the number, y, of bacteria present after t minutes, approximately what is the population after 90 minutes?
- 14,000
- 18,220
- 20,480
- 24,000
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to solve problems involving logarithmic and exponential functions. At t equals 0, y equals 5000, so 5000 equals C e to the zero power and C = 5000. Solve for k: 8000 is 5000 e to the power of 30 times k, which becomes eight fifths equals e to the power of 30 times k. Take the natural log of both sides: the natural log of eight fifths equals 30k and k is approximately 0.0157. For t equals 90, y equals 5000 times e to the power of 0.0157 times (90) so y is approximately 20,541.
Competency 0004
Calculus
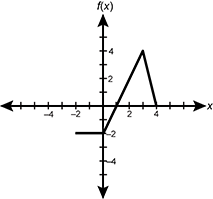
10. Use the graph below to answer the question that follows.
Graph straight line starting at, negative two, negative two staying constant until zero, negative two and starts increasing steadily passing through one, zero then continuing to increase up to three, four then decreasing steadily down to four zero.
The graph of a function
f of X
is shown above. What is the value of
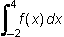 ?
?
- 1
- 5
- 6
- 11
- Enter to expand or collapse answer. Answer expanded
-
Correct Response: A. This question requires the examinee to interpret
a definite integral as a net area. The expression
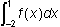 is the negative of the area below the x-axis. Using geometry, the area
is 4 for the square and 1 for the triangle, so
integral from negative 2 to 1 of f of x dx equals negative 5.
Similarly
integral from one to four of f of x dx equals 6,
the area of the triangle above the x-axis. Adding the two parts results in
integral from negative two to four of f of x dx equals negative 5 plus 6 equals 1.
is the negative of the area below the x-axis. Using geometry, the area
is 4 for the square and 1 for the triangle, so
integral from negative 2 to 1 of f of x dx equals negative 5.
Similarly
integral from one to four of f of x dx equals 6,
the area of the triangle above the x-axis. Adding the two parts results in
integral from negative two to four of f of x dx equals negative 5 plus 6 equals 1.
Competency 0004
Calculus
11. At what value of x does the graph of y equals open paren x plus 1 close paren quantity squared times the quantity x minus 2 have a relative minimum?
- x = negative2
- x = negative1
- x = 1
- x = 2
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. The examinee could use a graphing calculator to graph the function and find the x-value of the relative minimum point by inspection, table, trace, or calculation. If a graphing calculator is not used, this question requires the examinee to apply properties of derivatives to analyze the graphs of functions. The first derivative of a function can be used to find relative maximums and minimums. Using the product rule, y prime is open paren x plus 1 close paren quantity squared times 1 plus open paren x minus 2 close paren times open bracket 2 times open paren the quantity x + 1 close paren times 1 close bracket. Factor: y prime is open paren x plus 1 close paren times open bracket open paren x plus 1 close paren plus 2 times open paren x minus 2 close paren close bracket equals 3 times the quantity x plus 1 times the quantity x minus 1. Set y prime equal to zero to find critical points: x equals negative 1 or x equals 1. Look at the sign of the derivative on each of three intervals determined by the critical point values. When x is less than negative 1, y prime is greater than 0, so the function is increasing. When negative 1 is less than x is less than 1, y prime is less than 0, so the function is decreasing. When x is greater than 0, y prime is greater than 0, so the function is increasing. The relative minimum occurs when the function changes from decreasing to increasing at x equals 1.
Competency 0004
Calculus
12. Use the diagram below to answer the question that follows.
A lidless cylinder partially filled with water is shown. The depth of the water is labeled y. There is a hole along the bottom ring of the tank with an arrow pointing outward, which symbolizes the water leaving the cylinder.
A lidless cylindrical tank is filled with water. A small hole develops at the bottom of the tank, as shown in the diagram, and water leaks out. The instantaneous rate at which the water level y in the tank drops is directly proportional to the square root of the depth of the water at time t. Suppose that, at time t is 0 minutes, the depth y is 16 inches and the instantaneous rate at which the water level y changes is negative 4 inches per minute. Which equation expresses the depth y of water in the tank as a function of the time t since the water began leaking from the tank?
- y equals negative 1 times the square root of t plus 16
- y equals negative 2 times t plus 16
- y equals negative one-fourth t times the square root of t plus 16
- y equals one-fourth times t squared minus 4 t plus 16
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to model and solve problems involving first order differential equations. The instantaneous rate of change for the depth of the water is directly proportional to the square root of the depth y, so the instantaneous rate of change for the depth of the water equals k times the square root of y. Substitute to find k: negative 4 equals k times the square root of 16, so k equals negative 1. Separate variables to get y to the negative one half power d y is k times d t. Integrate both sides of this equation: 2 times y to the one half power is k t plus C. Substitute t equals 0, k equals negative 1, and y equals 16 to solve for C, which equals 8. The equation is now 2 times y to the one half power is negative 1 t plus 8. Divide both sides by 2 and square both sides of the result to get y is one-fourth times t squared minus 4 t plus 16.
Competency 0005
Geometry and Measurement
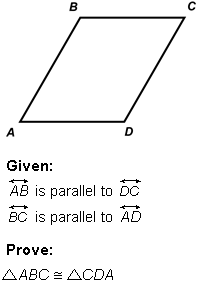
13. A student is assigned the following proof.
Parallelogram A B C D. Given that line A B is parallel to line D C, and line B C is parallel to line A D, prove that triangle A B C is congruent to triangle C D A.
The student reasons as follows:
Draw a line between point A and point C. Then, angle B C A is congruent to angle D A C. Also note that angle B A C is congruent to angle D C A Now, line A C is congruent to Line A C so the two triangles are congruent by angle-side-angle.
Which statement best justifies the second and third sentences in the student's response?
- If two lines are cut by a transversal and same-side interior angles are congruent, then the lines are parallel.
- If two lines are cut by a transversal and alternate interior angles are congruent, then the lines are parallel.
- If two parallel lines are cut by a transversal, then same-side interior angles are congruent.
- If two parallel lines are cut by a transversal, then alternate interior angles are congruent.
- Enter to expand or collapse answer. Answer expanded
- Correct Response: D. This question requires the examinee to apply theorems about lines and angles. line A C is a transversal intersecting line B C and line A D . angle B C A and angle D A C are alternate interior angles. Because these angles are formed by parallel lines, they are congruent. line A C is also a transversal intersecting line A B and . line D C The same reasoning holds for angle B A C and angle D C A
Competency 0005
Geometry and Measurement
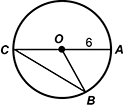
14. Use the diagram below to answer the question that follows.
A circle is shown with a radius of 6. A line segments passes from point C through the center of the circle, labeled point O, to point A. A third point on the circumference of the circle is labeled B and line segments extend to it from points O and C. The length of radius OA is 6 units.
Circle O has a radius of 6. The arc length of 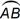 is 4 pi 3. What is the measure of angle O C B ?
is 4 pi 3. What is the measure of angle O C B ?
- 10 degrees
- 20 degrees
- 30 degrees
- 40 degrees
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to apply theorems about circles to solve a measurement problem. The circumference of circle O is 2 pi times 6, or 12 pi. The measure of arc AB is four-thirds pi divided by the quantity 12 pi, or one-ninth of the circumference of the circle. Arc AB represents one-ninth of 360 degrees, or 40 degrees of arc. The central angle AOB has the same degree measure as the arc it subtends. The inscribed angle ACB has a degree measure equal to one-half the degree measure of the arc it subtends, so the measure of angle OCB is 20 degrees.
Competency 0005
Geometry and Measurement
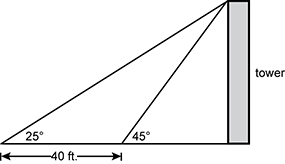
15. Use the diagram below to answer the question that follows.
Two triangles are shown. Both triangles share a common leg, labeled tower, and the bases of these triangles partially overlap; the base of larger triangle is 40 feet longer than the base of the shorter triangle. The angle from the base to the hypotenuse of the larger triangle is 25 degrees, while the corresponding angle in the smaller triangle is 45 degrees.
At a certain distance from the base of a tower, the angle of elevation of the top of the tower is 25 degrees. At a point 40 feet closer to the tower, the angle of elevation of the top of the tower is 45 degrees. Approximately how tall is the tower?
- 60 feet
- 42 feet
- 35 feet
- 19 feet
- Enter to expand or collapse answer. Answer expanded
- Correct Response: C. This question requires the examinee to apply right angle trigonometry. The triangle with a 40-foot leg includes a 25 degree angle. The two other angles are 135 degrees, which is supplemental to the 45 degree angle, and 20 degrees, which is the difference of 180 degrees and 25 degrees plus 135 degrees. The equation x over the sine of 25 degrees equals 40 over the sine of 20 degrees follows from the law of sines, where x is the length of the hypotenuse of the 45 degree right triangle; therefore, x is root 2 times larger than the height of the tower. The value of the x is about 49.4 feet, and so the height of the tower is about 35 feet, or 49.4 over root 2.
Competency 0006
Statistics and Probability
16. A bottling company uses a machine to fill juice bottles. The quantity of juice that goes into each bottle is normally distributed, with a mean of 471.5 milliliters and a standard deviation of 1.75 milliliters Approximately what percentage of the bottles receives less than 468 milliliters ?
- 1.75 percent
- 2.5 percent
- 3.5 percent
- 5 percent
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to demonstrate understanding of a normal probability distribution. Using the given mean and standard deviation, 471.5 minus 2 times 1.75 equals 468, so the values in question are more than 2 standard deviations below the mean. In a normal distribution, approximately 95 percent of the data falls within 2 standard deviations of the mean, so about 5 percent falls outside that region. Since the normal distribution is symmetric, 2.5 percent of the data falls more than 2 standard deviations above the mean and 2.5 percent falls more than 2 standard deviations below the mean.
Competency 0006
Statistics and Probability
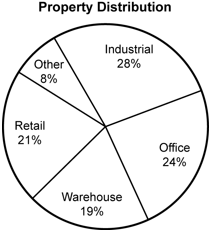
17. Use the circle graph below to answer the question that follows.
A circle graph illustrating the distribution of properties by their uses is shown. Industrial properties make up 28 percent of the distribution. Moving clockwise from that section: offices make up 24 percent of properties, warehouses 19 percent, retail 21 percent, and other 8 percent.
The circle graph shows the distribution of properties owned by a real estate investment trust company. If the company owns 336 industrial properties, how many retail properties does the company own?
- 228
- 252
- 288
- 312
- Enter to expand or collapse answer. Answer expanded
- Correct Response: B. This question requires the examinee to analyze data represented in a circle graph. The 336 industrial properties represent 28 percent of the total number of properties, t, so 336 = 0.28t. Solve this equation to find that t = 336 divided by 0.28 = 1200 properties. Then the total number of retail properties is 0.21 times 1200 = 252 properties.
Competency 0006
Statistics and Probability
18. The membership of a school club consists of 6 juniors and 9 seniors. Four members will represent the club at the school's open-house night. If the representatives are randomly chosen, what is the probability that 2 juniors and 2 seniors will represent the club?
- 36 over 91
- 8 over 27
- 6 over 91
- 2 over 27
- Enter to expand or collapse answer. Answer expanded
- Correct Response: A. This question requires the examinee to compute probabilities of compound events using combinations. Since there are 6 juniors, there are six times five over 2 ways to choose 2 juniors. Since there are 9 seniors, there are 9 times 8 over 2 ways to choose 2 seniors. For each of the 15 pairs of juniors, there are 36 pairs of seniors, so there are 15 times 36 or 540 different ways to choose 2 juniors and 2 seniors. If any 4 students are chosen, there are 15 times 14 times 13 times 12 divided by the product of 4, 3, 2, and 1, or 1365 different ways to choose them. The probability of choosing exactly 2 juniors and 2 seniors is 540 divided by 1365 or 36 over 91.

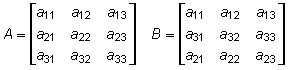
 cos
cos
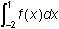 = –5.
= –5.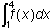 = 6,
= 6,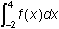 = –5 + 6 = 1.
= –5 + 6 = 1.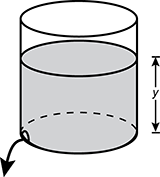
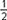 . Substitute to find k: −4 = k√
. Substitute to find k: −4 = k√