Study Guide
Field 222: Multi-Subject: Teachers of Childhood
(Grade 1 to Grade 6)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Constructed-Response Item 1
Competency 0005
Analysis, Synthesis, and Application
Use the information provided in the exhibits to complete the task that follows.
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Background Information
Fourth-grade students have been developing an understanding of fractions. The class has reviewed representing numbers on a number line, worked with equivalent fractions in special cases, and compared fractions by reasoning about their size. The class is currently working on the following standard from the New York State Learning Standards for Mathematics.1 footnote 1
Number & Operations—Fractions (NY-4.NF)
Extend understanding of fraction equivalence and ordering.
2. Compare two fractions with different numerators and different denominators.
Recognize that comparisons are valid only when the two fractions refer to the same whole.
Record the results of comparisons with symbols greater than, equals sign, or less than, and justify the conclusions.
In particular, the teacher has planned a lesson experience in which students will use benchmarks to compare and order fractions. The students have worked with halves, fourths, eighths, thirds, sixths, and twelfths. The teacher has the students work in groups of two.
Description of Class Activity
The teacher gives each pair of students a set of "benchmark cards." Each card is a shaded index card labeled with the number 0, or 1. The students place the benchmark cards in correct order from least to greatest along a number line drawn on a piece of cardboard.
Each pair of students also has a pack of "fraction cards." Each card is an unshaded index card labeled with a fraction (e.g., six sixths , one fourth , two thirds , three halves , five twelfths , four eighths ). Each student takes a turn selecting a fraction card from the pack. A card that is equal to one of the benchmark cards is placed beneath the benchmark card. The remaining cards are placed between the benchmark cards in the correct order.
While working with their partner, students are encouraged to justify the placement of each card by reasoning about fraction equivalencies and relationships. The student placing the card must explain his or her reasoning while the student observing is encouraged to question and critique the partner's decisions. The teacher has emphasized that both partners will need to be prepared to justify the placement of fractions on the number line.
Excerpt of Interview with Student
As students work, the teacher moves among them and asks questions that require students to explain their reasoning about comparing and ordering fractions. The teacher stops to observe one group's work in progress and asks one of the students several questions. The group's work is shown below, followed by a short excerpt of the discussion between the teacher and the student.
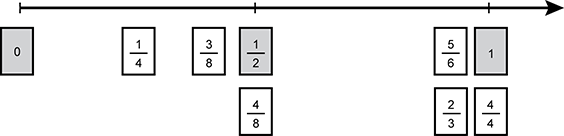
A series of fractions ordered from smallest to largest on a number line. From left to right, zero, one fourth, three eights, one half and four eights are in the same position, five sixths and two thirds are in the same position, one and four fourths are in the same position.
Teacher: How did you and your partner decide where would go on your number line?
Student: Well, we put four eighths under one half because we know they are equal. So then we knew that three eighths must be less than one-half because you need one more piece to make it one half . We also know that three eighths is larger than one fourth because one fourth is the same as two eighths . Teacher: How did you decide where to place five sixths and two thirds on your number line? Student: We know that five sixths is more than one-half because it only takes three sixths to equal one half . And two thirds is the same as five sixths because you just need one more piece to make them both a whole. Teacher: Can you show me what you mean when you say, "you just need one more piece"? Student: Well, if I think about a pie, I know I only need one more piece to make the whole. Teacher: Can you show me what you are thinking of with a drawing? Student: That's easy! I'll make two pies. One shows five sixths and one shows two thirds . Two shaded pie charts; one represents five sixths, the other two thirds. One sixth and one third, respectively, are unshaded in each chart.
Student: See, they both have one piece missing so they are both the same and they must be pretty close to one whole.
Sample Strong Response to Constructed-Response Item 1
A strength that the student demonstrates is understanding that fractions with different numerators and denominators can be equivalent. This is shown by the statement, "we put four eighths under 1 half because we know they are equal" and later by " 1 fourth is the same as 2 eighths ." The student could compare fractions that have the same denominators, showing an understanding of the meaning of the numerator. The statement " because you need one more piece to make it 1 half, " although lacking in precise terminology, was accurately used to explain that 3 eighths was less than 4 eighths.
A significant area of need is demonstrated in the student's lack of understanding that denominator determines piece size. When comparing fractions with different denominators, the student made no distinction between the size of the pieces that are being considered; he considered only the number of pieces. This is illustrated by the statement " 2 thirds is the same as 5 sixths because you just need one more piece to make them both a whole." Although the student was able to draw both fractions as a pie and shade the correct number of pieces, he apparently did not discern that the missing piece in the pies were different in size, and that, in fact, the pies themselves were not the same size. He noted only that there was one piece missing from each and erroneously concluded that the fractions were equivalent.
Instructional intervention should start with the student using strips of paper to fold and create fraction strips for a variety of fractions (thirds, fourths, sixths, eighths) and to compare 2 thirds to 3 fourths and to 5 sixths. The teacher would ask are they all equal? Which of the three is closest to one whole? Compare the amount left to make one whole. Are 1 third, 1 fourth, and 1 sixth equal? Why not? What is the meaning of the denominator in a fraction? What does it tell you?
Using fraction strips, the student could then be asked to compare several fractions that have the same numerator but different denominators, such as 2 sixths and 2 fourths or 5 eighths and 5 sixths Because the student appears to have some understanding of equivalent fractions, the next step would be to do work converting 2 thirds and 5 sixths to fractions with common denominators. The teacher would ask for a comparison of the new fractions, written with common denominators, to each other. Then the student should compare several other pairs of fractions "with one piece missing" in the same manner, finding common denominators. As he works, he should explain his process and his thinking to the teacher.
Students using symbolic notation for fractions may get lost in the symbols and fail to remember that denominators define the size of the fractional part and numerators represent the number of this part. The use of a visual model (the strips) coupled with teacher questioning and student explanations, would help a student to understand key concepts, thus enabling him to build a viable argument regarding equivalent fractions, and allowing him to progress to new ideas.
Sample Constructed-Response Item 2
Competency 0005
Analysis, Synthesis, and Application
Use the information provided in the exhibits to complete the task that follows.
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by a student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the given standard that is demonstrated by the same student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student improve in the identified area of need. Include a strategy for helping the student build a viable argument related to the given standard.
Background Information
Second-grade students have been developing an understanding of coin values. The class has learned the values of quarters, dimes, nickels, and pennies, and has been using skip-counting to determine the value of mixed groups of coins. The class is currently working on the following standard from the New York Learning Standards for Mathematics.2 footnote 2
Measurement and Data (NY-2.MD)
Work with time and money.
8a. Count a mixed collection of coins whose sum is less than or equal to one dollar.
The teacher has planned a learning experience called "Coin Caterpillars" in which students will create the "body" of a caterpillar by choosing coins that sum to the value noted on the caterpillar's "head."
Description of Class Activity
The teacher draws a caterpillar head on a sheet of paper and writes the value 32 cents inside the head. Using a document camera to project the image, the teacher demonstrates to students how to use plastic replicas of coins to create the body of the caterpillar so that the values of the coins sum to the value written on the inside of the caterpillar's head, as shown:
Manipulatives in the shape of a caterpillar are shown. A circle represents a caterpillar head with 32 cents written inside it. The body of the caterpillar is made of 4 coins. From left to right the coins are quarter, nickel, penny, penny.
After the class practices creating two more caterpillars as a group, the teacher then provides pairs of students with several plastic replicas of quarters, dimes, nickels, and pennies. Students also receive a "Coin Caterpillars" worksheet where the values on the inside of the caterpillar heads are given. The teacher then instructs the students to use their coin replicas to create the bodies of the caterpillars shown on their worksheets. The teacher tells them to individually create the body of each caterpillar and to then check each answer with their partner before moving on to the next caterpillar body.
Excerpt of Interview with Students
As the students work, the teacher moves among them in order to observe their progress. One pair of students becomes loud as they debate their answer. One pair of students' work is shown below, followed by a short excerpt of a discussion between the students and the teacher.
Student work with manipulatives in the shape of two caterpillars is shown.

Student 1's work has a circle that represents a caterpillar head with 56 cents written inside it. The body of the caterpillar is made of 4 coins. From left to right the coins are quarter, quarter, nickel, penny.

Student 2's work has a circle that represents a caterpillar head with 56 cents written inside it. The body of the caterpillar is made of 11 coins. From left to right the coins are dime, dime, dime, dime, dime, penny, penny, penny, penny, penny, penny.
Student 1: We have the same answer! Student 2: No, we don't! It's not the same! Student 1: Yes, it is! Look, I have 25, 50, 55, 56. You have 10, 20, 30, 40, 50, 51, 52, 53, 54, 55, 56. We both get 56. It's the same. Student 2: No, it's not. Teacher: Hey, you two. What's going on here? Student 1: I think we have the same answer—we both have 56—but he's saying I'm wrong. Student 2: I have more than he does, so one of us is wrong. Teacher (to Student 2): Why do you say that you have more than he does? Student 2 (pointing): Look. He only has 1, 2, 3, 4. Right? He's got 4 coins. I have 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Eleven is more than 4. Student 1: Yeah, you have more coins, but your coins and my coins add up to the same thing. Teacher (to Student 1): Explain what you mean by that. Student 1: So I have 2 quarters, and that equals— Student 2: Fifty cents. Yeah, that's what I got. Student 1 (to Student 2): That's because you have 5 dimes. Student 2: I know. Student 1: So 2 quarters is 50 cents, but so is 5 dimes. It's the same thing. It's like, my 2 quarters are the same as your 5 dimes, and my nickel and penny are the same as your 6 pennies. They both equal 6 cents. Teacher: It sounds like you're saying the value of each coin needs to be looked at.
Sample Strong Response to Constructed-Response Item 2
Student 2 has a significant strength in being able to count by tens. This is illustrated when the student uses 5 dimes to begin his coin caterpillar. By using the 5 dimes, he is able to illustrate 50 cents. He is then able to count up from there, using pennies, placing 6 pennies on the body of the caterpillar to make 56 cents. He successfully answers the math problem given to him.
A significant need for this student seems to be his ability to apply the concept that different coins can be used to obtain the same monetary amount. Student 2's caterpillar has 11 coins, while Student 1's has only 4 coins, which leads Student 2 to believe that the total amounts are not the same. His understanding is too concrete, in that he does not yet understand that one set of coins added together can represent the same value as another set of coins, even if the number of actual coins is different.
Since the student seems to understand skip-counting as evidenced in his counting by tens using dimes, I would start by asking the student to show me 50 cents while just using pennies. He knew to count six pennies for the problem shown, so he should also be able to count out 50 pennies to represent 50 cents. I would then have him do the same with nickels as well as with dimes. As he does this, we will observe together how many coins are in each representation of 50 cents. I would then ask him to skip-count with nickels to make a total of 25 cents, and set this series of coins next to a quarter, to illustrate two different ways to make 25 cents. I would have him build a "caterpillar" of 50 cents, using the fewest number of coins to do so and, ideally, he will see that this would be done using two quarters. From there, I would have him add 6 cents to this caterpillar, again using the fewest number of coins, making it similar to the 56-cent caterpillar Student 1 created earlier. Once this is grasped, I would have him create a series of "caterpillars" using a variety of coins, to see how many different ways he could create a caterpillar for the same total amount of money. Perhaps I could have him create three caterpillars for each series of amounts given (47 cents, 74 cents, 60 cents, for example) and then ask him to use skip-counting to explain how these caterpillars actually represent the same amount of money, even if the number of coins are different for each caterpillar. Having the student practice making similar monetary values, using a variety of coins, and having him explain, or skip-count, to prove the value, should help him to see that money values can be represented in many ways, depending on the value of the coin.
Performance Characteristics for a Constructed-Response Item
The following characteristics guide the scoring of the response to a constructed-response item.
| Completeness | The degree to which the response addresses all parts of the assignment |
|---|---|
| Accuracy | The degree to which the response demonstrates the relevant knowledge and skills accurately and effectively |
| Depth of Support | The degree to which the response provides appropriate examples and details that demonstrate sound reasoning |
Score Scale for a Constructed-Response Item
A score will be assigned to the response to a constructed-response item according to the following score scale.
| Score Point | Score Point Description |
|---|---|
| 4 |
The "4" response reflects a thorough command of the relevant knowledge and skills:
|
| 3 |
The "3" response reflects a general command of the relevant knowledge and skills:
|
| 2 |
The "2" response reflects a partial command of the relevant knowledge and skills:
|
| 1 |
The "1" response reflects little or no command of the relevant knowledge and skills:
|
| U | The response is unscorable because it is unrelated to the assigned topic or off task, unreadable, written in a language other than English or contains an insufficient amount of original work to score. |
| B | No response. |
Acknowledgments
1From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Internet. Available from http://www.nysed.gov/curriculum-instruction/new-york-state-next-generation-mathematics-learning-standards; accessed 2/20/2019.
2Ibid.

