Study Guide
Field 244: Multi-Subject: Secondary Teachers
(Grade 7–Grade 12)
Part Two: Mathematics
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Sample Constructed-Response Item 1
Competency 0004
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the task that follows. end bold
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student meet the area of need you identified above. Include a strategy for helping the student build a viable argument related to the given learning standard.
Exhibit 1: Background Information
A teacher is working with a student in a high school geometry class. The class is currently working on the following standard from the New York State Learning Standards for Mathematics.1
start bold Similarity, Right Triangles, and Trigonometry G-SRT end bold
start bold Understand similarity in terms of similarity transformations end bold
2. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar. Explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. Note: With dilations or rotations, the center of the transformation must be specified.
In particular, the class is extending their knowledge of similar triangles to identifying other similar polygons. Previous work has included formal and informal definition of the concept of similarity as well as practice identifying similar triangles in a variety of orientations.
Exhibit 2: Student Work Sample
After a whole class review of what similarity means and how to identify it, students are working to identify which pairs of presented polygons are similar. The following exhibit shows three sample problems from the student's work along with the student's response to each question. Both the problems and the responses are representative of the student's work.
start bold Worksheet Directions: Determine whether or not the two polygons are similar and explain your reasoning. end bold
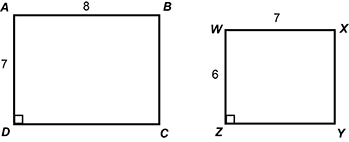
Problem 1:
Two quadrilaterals that visually appear to be rectangles are shown. Quadrilateral A B C D has a right angle at angle D, and has side A D of length 7 and side A B of length 8. Quadrilateral W X Y Z has a right angle at angle Z, and has side W Z of length 6 and side W X of length 7.
Similar, because they are both rectangles and there is the same relationship between the sides
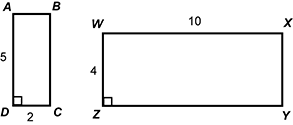
Problem 2:
Two quadrilaterals that visually appear to be rectangles are shown. Quadrilateral A B C D has a right angle at angle D, and has side A D of length 5 and side D C of length 2. Quadrilateral W X Y Z has a right angle at angle Z, and has side W Z of length 4 and side W X of length 10.
Not similar, because even though they are both rectangles, the sides are not related
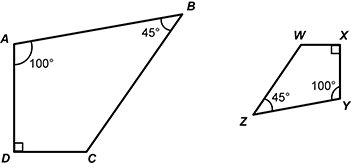
Problem 3:
Two quadrilaterals are shown. Quadrilateral A B C D has a right angle at angle D, a 100 degree angle at angle A, and a 45 degree angle at angle B. Quadrilateral W X Y Z has a right angle at angle x, a 100 degree angle at angle Y, and a 45 degree angle at angle Z.
Similar, because all the angles are the same, so the sides have to have the same relationship
Exhibit 3: Excerpt of Interview with Student
The following is an excerpt of an interview between the teacher and the student in which the teacher questions the student about the method of solution used to solve the problems shown in Exhibit 2.
Teacher: How did you decide whether or not the two figures in Problem 1 were similar? Student: Well, I know that similar triangles have to have all the same angle measurements and that the sides have to be related to each other in the same way, so I think that must hold for these other shapes. So these ones are both rectangles, meaning that all their angles are the same, plus I see that if you add one to 7 you get 8 in the first rectangle and if you add one to 6 you get 7 in the second. That means they have the same relationship, so they must be similar. Teacher: What about in Problem 2? Student: Again, they are both rectangles, so all the angles are 90 degrees and the same. But when I look at the sides, even if I flip the second rectangle so it looks the same, I have to add three to get from 2 to 5 in the first but have to add six to get from 4 to 10 in the second. So they don't have the same relationship and can't be similar. Teacher: And how about Problem 3? Why did you say that they were similar? Student: This one was easy—all the angle measurements were the same, so even though there aren't any side measurements, the funny shape means that everything is going to match up and they must be similar. Teacher: Why does the shape have anything to do with it? Student: Well, like for the rectangles... you have to look at the sides because you can stretch a rectangle without changing the angles. For shapes like this, it must be like the triangles, where if you stretch a side, you would change an angle. So everything has to be stretched the same amount to keep the same angles, and that means that it's proportional.
Sample Strong Response to Constructed-Response Item 1
One strength that the student exhibits is that he recognizes that when dilating a figure, keeping two figures similar, the angles need to stay the same, and the sides need to change proportionally to the original figure. In his explanation regarding similarity in problem 3, the student states that the figures are "similar, because all the angles are the same, so the sides have to have the same relationship." He also states this in his explanation to his teacher. Regarding problem 1, he states, "…similar triangles have to have all the same angle measurements and that the sides have to be related to each other in the same way…" and when discussing problem 3, "…everything has to be stretched the same amount to keep the same angles, and that means that it's proportional."
While he understands this, with respect to similarity, he has a misunderstanding of how proportionality is determined. In Problem 1, he states that the figures are similar because they're both rectangles and that the relationship between the sides is similar. He states this regarding problem 3, as well. With problem one, he tells the teacher that adding 1 to 7 is 8, and adding 1 to 6 is 7, so therefore the sides had the same relationship. Regarding problem 2, he states that the shapes can't be similar because he cannot add the same number to both and get the lengths of the second rectangle. In the 3rd problem, he tells the teacher that the sides are proportional, but without any dimensions, he cannot prove that they are in proportion, only that they look like they are. He is unclear as to how proportionality is determined and, based on his responses, he appears to think that it's determined using addition or subtraction instead of multiplication or division.
To help this student understand similarity, I'd start by pointing out that he already has an understanding of the need for the angles to be the same, as well as for the sides to be in proportion with the corresponding figure, and that we are going to expand on this understanding with practice. I would have him work with a computer program, which will dilate the rectangle, to see if, when he does this with the second shape in problem one, he's able to get a shape similar to the first rectangle (can you dilate the rectangle with the sides of 6 and 7, and create a shape with sides of 7 and 8?). He'll see that this isn't possible. I would then talk to him about how we determine whether the sides are in proportion with each other, reminding him that we determine this using division (ratios) and not addition, which is how he has erroneously come to the conclusion that these shapes are similar. I would have the student put the corresponding sides from both rectangles into a proportion, and check to see if the proportion is true. For example, in problem 1, A D divided by W Z equals 7 divided by 6 and A B divided by W X equals 8 divided by 7, and set them equal, to find the cross product 7 divided by 6 equals 8 divided by 7. He will find that this equates to 99 equals 98 which isn't equal and therefore not in proportion. Doing the same with problem 2, he'll see that the two figures are similar. I'll have the student work with me, or a partner, to dilate shapes using the computer program, and determine the proportionality using cross multiplication of the fractions created. As he does this, I'll have him discuss his findings, about whether the various shapes are similar. Extended practice with these methods, should help solidify the student's understanding and help him explain how this relationship is determined.
Sample Constructed-Response Item 2
Competency 0004
Analysis, Synthesis, and Application
start bold Use the information provided in the exhibits to complete the task that follows. end bold
Using the data provided, prepare a response of approximately 400 to 600 words in which you:
- identify a significant mathematical strength related to the given standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment;
- identify a significant area of need related to the standard that is demonstrated by the student, citing specific evidence from the exhibits to support your assessment; and
- describe an instructional intervention that builds on the student's strengths and that would help the student meet the area of need you identified above. Include a strategy for helping the student build a viable argument related to the given learning standard.
Exhibit 1: Background Information
A teacher is working with a student in a high school algebra class. The class is currently working on the following standard from the New York State Learning Standards for Mathematics.2
Reasoning with Equations and Inequalities AI-A.REI
Solve equations and inequalities in one variable.
4b. Solve quadratic equations by:
roman numeral 1 inspection,
roman numeral 2 taking square roots
roman numeral 3 factoring
roman numeral 4 completing the square,
roman numeral 5 the quadratic formula, and
roman numeral 6 graphing.Recognize when the process yields no real solutions.
In particular, the class is working on solving quadratic equations by factoring. Previous classes have covered the structure of expressions, writing expressions in equivalent form, and performing arithmetic with polynomials.
Exhibit 2: Student Work Sample
The student was asked to solve several quadratic equations by factoring. Shown below are two sample problems along with the student's response to each problem. Both the problems and the responses are representative of the student's work.
start bold Worksheet Directions: Solve for x. Check your work and justify the steps you used to find the solution. end bold
start bold Problem 1: end bold x squared + 2 x minus 3 equals 0
x squared plus 2 x minus 3 equals 0
factor this
x times x
look at negative 3
negative 3 times 1 equals negative 3 3 times negtaive 1 equals negative 3
3 plus negative 1 equals 2
left paren x plus 3 right paren left paren x minus 1 rigth paren equals 0
left paren x plus 3 right paren left paren x minus 1 right paren equals
equals x times x plus x times negative 1 plus 3 x times negative 1
equals x squared minus x plus 3 x minus 3
solve each of these for x
left paren x plus 3 right paren
x plus 3 equals 0
start underline, minus 3, minus 3, end underline
x equals negative 3
left paren x minus 1 right paren
left paren x minus 1 right paren equals 0
x minus 1 equals 0
start underline, plus 1, plus 1, end underline
x equals positive 1check answer
x equals negative 3
x squared plus 2 x minus 3 equals 0
left paren negative 3 right paren squared plus 2 left paren negative 3 right paren minus 3
9 minus 6 minus 3
0 equals 0, checked
x squared plus 2 x minus 3 equals 0
left paren positive 1 rigth paren squared plus 2 left paren positive 1 right paren minus 3 equals 0
1 plus 2 minus 3 equals 0
0 equals 0, checked
You find the solution by solving the equation. Plug the answer back into the equation to check it.
Problem 2: x squared plus 6 x equals negative 8
to factor this
take out an x
x squared plus 6 x equals negative 8
left paren x right paren left paren x plus 6 right paren equals negative 8Now you can solve it.
x equals negative 8
left paren x plus 6 right paren
x plus 6 equals negative 8
6 equals 6 x equals negative 2check
x squared plus 6 x equals 8 gives you
left paren 8 right paren squared plus 6 left paren 8 right paren which becomes
64 plus 48 then
112x squared plus 6 x gives you
left paren negative 2 right paren squared plus 6 left paren negative 2 right paren gives you
4 plus 12 gives you
16Since this is an equation, both sides must be equal, so you set them equal to each other and solve for x.
Exhibit 3: Excerpt of Interview with Student
The following is an excerpt of an interview between the teacher and the student in which the teacher questions the student about the method of solution used to solve the problems shown in Exhibit 2.
Teacher: We will start with Problem 1. Can you tell me what you did to solve this equation? Student: First I wrote down two sets of parentheses. Then I factored it by looking for two numbers that when multiplied give 3, no, minus 3, and when you add them you get 2. I wrote out possible answers and found that 3 and minus 1 worked. Then I put them in with the x's like here (points to the product of two binomials set equal to zero). Teacher: It looks like after you factored the trinomial into two binomials, you set each of them equal to zero and solved the resulting equation. Can you tell me why you took that step? Can you justify why you set each binomial equal to zero? Student: Whatever is on the left side of the equation has to equal what's on the right side. So left paren x plus 3 right paren has to equal zero and so does left paren x minus 1 right paren, because equations have to balance. Then you just add or subtract the number to find the answer. Teacher: Let's look at Problem 2. Can you tell me what strategy you used to solve the equation? Student: I solved it just like I solved the first one. This time, though, it was easier to solve because it's easier to factor. You just take out an x. Teacher: After you factored the left side of the equation, what did you do next? Student: I set both sides of the equation equal to 8 and solved for x. Teacher: Can you justify why you took that step? Student: Both sides of an equation must be equal. So whatever is on the left side has to equal what is on the right side. So I set them equal to each other and solved for x.
Sample Strong Response to Constructed-Response Item 2
A significant strength demonstrated by the student is her understanding of how to factor a polynomial. When factoring Problem 1, the student knew two numbers were needed that "when multiplied give minus 3, and when you add them you get 2" as the constant terms in the binomials. Although she made many errors in Problem 2, she correctly factored x squared plus 6 x equals negative 8 as left parentheses x right parentheses left parentheses x plus 6 right parentheses equals 8.
One significant need demonstrated by the student is her misunderstanding of the Zero Product Property. A zero product indicates that at least one of the factors must also equal zero. The student demonstrates an incomplete understanding of this property in the interview when she explains that both ( x plus 3) and ( x minus 1 ) have to equal zero "because equations have to balance." She then apparently generalizes this flawed understanding and incorrectly concludes that a product other than zero must have factors equal to that number, as shown in Problem 2: "x equals negative 8" and "x plus 6 equals negative 8" and her explanation that "I set both sides of the equation equal to 8" because "both sides of an equation must be equal." The student may not know the reason for factoring, and is simply factoring the polynomials because the assignment was "solve several quadratic equations by factoring."
Instructional intervention should start with the Zero Product Property. This concept is pivotal in understanding how and why to use factoring as a solution method for quadratic equations. The teacher could ask her to identify a list of possible solutions for A and B in the problem A times B equals zero. Then ask for a list of possible solutions for A and B in the problem A times B equals 12. The student will then compare the lists. The teacher should question the student to help her understand the property: What does she notice? Which list is easier to create and why? What is special about the number 0 when you are finding factors?
Next, ask the student to solve a problem such as this: left paren x plus 8 right paren left paren x minus 2 right paren equals zero. The student will probably solve this correctly, as she correctly solved left paren x plus 3 right paren left paren x minus 1 right paren equals 0 in Problem 1. The teacher should draw her attention to the similarity in her approaches to this problem and the previous A times B equals 0 problem.
Next, ask the student to solve a quadratic equation such as x squared minus 5 x plus 4 equals 0. The student would likely factor it correctly, as she has already shown her ability to factor. This time, as she set each factor to equal zero, the teacher would have her explain why she is doing that. Next, the student would be given an equation such as x squared plus 5 x equals negative 6. Drawing the student's attention back to the original A times B problems, the teacher would elicit the observation from the student that it was easier to solve the equation when the product was zero rather than another number because she knew that one of the factors would have to equal zero, and then guide the student to write an equivalent expression with a product of zero before solving.
Working from what she already knows (how to factor), the student will begin to build a viable argument for factoring as a solution method for quadratic equations as she comprehends the mathematical concept (the Zero Product Property) that underlies all the problems, from simple to more complex. To help her continue to build a viable argument, the teacher should give her a few more problems (some set up with the product set at zero, some with a product set as non-zero) and have her explain her steps and solutions.
Performance Characteristics for a Constructed-Response Item
The following characteristics guide the scoring of the response to a constructed-response item.
| Completeness | The degree to which the response addresses all parts of the assignment |
|---|---|
| Accuracy | The degree to which the response demonstrates the relevant knowledge and skills accurately and effectively |
| Depth of Support | The degree to which the response provides appropriate examples and details that demonstrate sound reasoning |
Score Scale for a Constructed-Response Item
A score will be assigned to the response to a constructed-response item according to the following score scale.
| Score Point | Score Point Description |
|---|---|
| 4 |
The "4" response reflects a thorough command of the relevant knowledge and skills:
|
| 3 |
The "3" response reflects a general command of the relevant knowledge and skills:
|
| 2 |
The "2" response reflects a partial command of the relevant knowledge and skills:
|
| 1 |
The "1" response reflects little or no command of the relevant knowledge and skills:
|
| U | The response is unscorable because it is unrelated to the assigned topic or off task, unreadable, written in a language other than English or contains an insufficient amount of original work to score. |
| B | No response. |
Acknowledgments
1From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Internet. Available from http://www.nysed.gov/curriculum-instruction/new-york-state-next-generation-mathematics-learning-standards; accessed 1/8/2019.